Механика современного дверного замка

Дверь захлопывается, и почти мгновенно возникает гнетущее чувство чего-то забытого. Но что? О нет!
В какой-то момент нашей повседневной жизни почти все мы задались вопросом, как открыть замок без свободного доступа к подходящему ключу.

Будь то, что мы забыли или потеряли этот ключ, или что мы никогда не владели им, открытие этого замка может быть чем угодно, от загадочной загадки до насущной необходимости. Вездесущие и все же источающие секретность замки действительно вызвали интерес у многих, в том числе знаменитых магов [29] и нобелевских лауреатов [40]. Неудивительно, что есть множество литературы, обучающей любителей и профессионалов внутренним органам замков и тому, как обходить их механические защитные механизмы, см., например, [44, 48, 51].

В то время как электронные замки становятся все более доступными, механические замки остаются стандартом де-факто во многих средах [32, 38]. Столкнувшись с толпой любительских и профессиональных открывателей (например, вскрытие замков сейфов Практик), слесарь должен изобрести и тщательно спроектировать комбинацию механических защитных механизмов. Они устанавливают требуемые функции управления в цилиндровом замке, чтобы разрешить доступ авторизованным ключам и запретить несанкционированные, а также противостоять взломам. Со временем значительно изменившись [51], «обычный» дверной замок в настоящее время может содержать множество крошечных механических устройств, изготовленных с высокой точностью при допусках микрометрового масштаба, см. Рисунок 1.1.

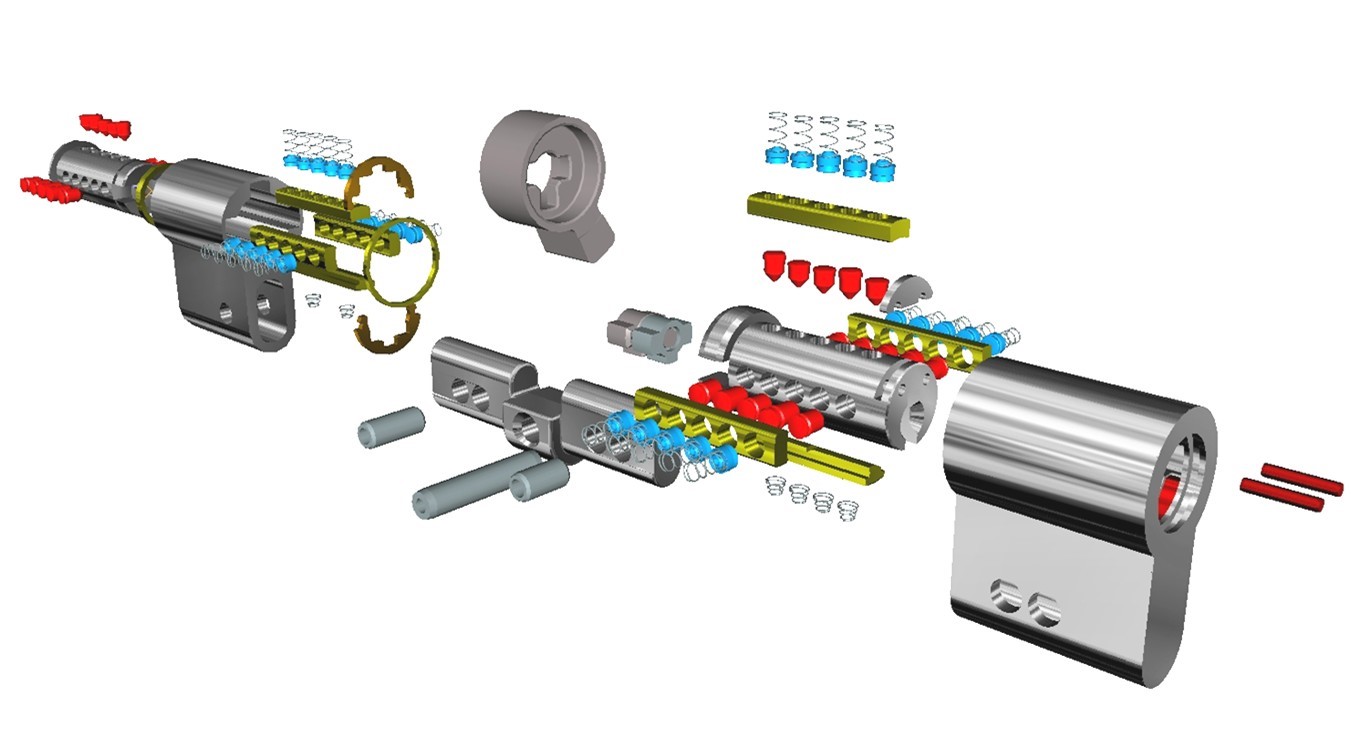
Рисунок 1.1. Точная механика внутри современного дверного замка. Между двумя цилиндрами расположен стопорный болт, механизм безопасности основан на подпружиненных массивах штифтов. Более подробная информация о технологии блокировки приведена в разделе 2. Изображение предоставлено компанией ASSA ABLOY (Швейцария) Ltd.

Механические цилиндрические замки имеют ряд сложных конструктивных ограничений, с которыми необходимо тщательно взвешивать требования безопасности. Помимо очевидных производственных затрат, наиболее ограничивающими ограничениями цилиндра являются его размеры (высота, ширина и глубина), которые определяются его окружением (например, дверью), а также отвращение людей к слишком большим или слишком тяжелым клавишам. Кроме того, для защиты от износа (например, от частого использования, загрязнения или изменения климата) любая механическая защитная функция должна быть особенно долговечной и не должна быть слишком маленькой. Таким образом, максимальное пространство, доступное внутри цилиндра, и минимальный размер механических устройств ограничивают количество защитных элементов, которые можно поместить в цилиндр.

Большое значение для этой статьи имеет еще одно несколько менее очевидное, но не менее сложное осложнение, а именно то, что обычно замки не существуют изолированно. Большинство замков происходят как часть систем замков, то есть ансамблей замков, которые концептуально и функционально связаны друг с другом. В качестве простого «игрушечного» примера рассмотрим двухэтажный дом на две семьи, в котором каждый из двух квартир имеет свой собственный дверной замок. Каждый замок должен быть открыт ключом жителя, но не должен открываться ключу другого подразделения. Уборка и управление, однако, должны быть в состоянии открыть обе двери.

Имея под рукой пример дуплексного дома, мы можем сразу же обнаружить множество более разнообразных и сложных систем замков, встречающихся, например, в квартирных или офисных зданиях, гостиницах, больницах или университетах. Их определяющими характеристиками являются два дополнительных набора, цилиндры и ключи, где каждый ключ должен открывать один или несколько цилиндров, но не должен открывать другие, и где каждый цилиндр должен быть разблокирован некоторыми ключами, но не должен быть разблокирован с помощью ключа. другие.

Типичная абстрактная спецификация системы замков, следовательно, состоит из прямоугольной таблицы A, где запись A (i, j) указывает, должен ли / не должен разблокироваться цилиндр i клавишей j. Таким образом, для системы электронных замков было бы достаточно сохранить эту таблицу в двоичном виде и просто проверить привилегии доступа из-за записи A (i, j), когда ключ j представлен в электронном замке i. Однако для механических замков таблица A должна быть неявно закодирована при выборе элементов защиты для каждого цилиндра и каждого ключа, поскольку ее размер обычно намного превышает доступное пространство. Кроме того, кодирование должно быть как можно более компактным, чтобы эффективно использовать ограниченное пространство цилиндров, а также экономить ресурсы и тем самым снижать затраты.

Для первого взгляда рассмотрим таблицу 1.1 и предыдущий пример дуплексного дома.

Таблица 1.1

Таблицы спецификаций для двух цилиндров дверей квартир С1 и С2, а также двух ключей жителей I1 (открытие С1, но не С2) и I2 (открытие С2, но не С1) и управляющего ключа М (открытие как С1, так и С2). «1» означает, что должен открываться, «0» означает, что не должен открываться.

Не желая углубляться в особенности механики, мы можем думать о протоколе «вызов-ответ», в котором мы моделируем функцию безопасности как часть «вызова» для любого ключа. Ряд таких функций размещен в различных местах в цилиндре, и если ключ «отвечает» на все из них правильно, то есть ключ обладает действительным «совпадающим двойником» в каждом из необходимых мест, цилиндр разблокируется или открывается. Обратите внимание, что абстрактное моделирование механики не только позволяет нам эффективно рассуждать, но и учитывает постоянное развитие механического дизайна из-за улучшенных производственных допусков и материалов, а также новых проблем, таких как проблема, возникающая при 3D-печати для защиты от копирования. защита.

Пример дуплексного дома достаточно прост, чтобы рассуждать о наименьшем наборе функций безопасности, необходимых для реализации спецификации в таблице 1.1. Если цилиндр С1 имеет элемент в положении А, но отсутствует в другом положении В, т. Е. [A B]: = [10], а цилиндр С2 выполнен с дополнительным элементом в положении В, но не с А, то есть [A B]: = [0 1] ’, затем клавиша I1 с двойными функциями« [1 0] »открывает только C1, но не C2, а клавиша I2 с« [0 1] »открывает только C2, но не C1. Ключ управления M будет «[1 1]» и откроет и C1, и C2. (Обратите внимание, что для того, чтобы гарантировать эти отношения, каждому из двух цилиндров потребуется только наличие собственной отличительной особенности, а не проверка других.)

Присвоение каждому цилиндру его собственной отличительной особенности указанным выше способом всегда допустимо, хотя и неэффективно, поскольку ограниченное пространство внутри цилиндров очень быстро истощается. К счастью, этого сценария можно избежать во многих практически актуальных случаях. Например, наиболее компактный подход для аналогичного «quinplex» дома с пятью квартирами, каждый из которых доступен по своему собственному ключу и ключу управления, требует только четырех, а не пяти функций безопасности. Любопытный читатель может сделать здесь короткую паузу, найти решение, а также обдумать связанные с этим проблемы, такие как общий дом n-plex. В целом, чем больше система блокировки и чем сложнее должна открываться / не открываться связь, тем труднее становится оптимально использовать ресурсы; Анализ сложности показывает, что оптимальной задачей кодирования является NP hard, см. [11, 27, 28, 36, 52].

Чтобы физически реализовать реальную систему замков, мы в конечном итоге должны вернуться к вопросу о механической выполнимости. Из-за вышеупомянутых требований к минимальным размерам, а также их конкретной формы, механические защитные элементы не могут быть произвольно размещены внутри цилиндра. Например, наличие объекта в одном месте не позволяет расположить другие слишком близко друг к другу. Таким образом, мы должны были бы найти механически подходящие места для всех необходимых защитных элементов в цилиндрах. Однако по практическим и материально-техническим причинам производители обычно начинают с другого угла и сначала рассматривают стандартизированные наборы физически возможных конфигураций цилиндров. В этом случае нам нужно найти подмножество цилиндров, которое достаточно богато, чтобы удовлетворить потребности имеющейся системы блокировки, то есть мы должны правильно выбрать механические соответствия для каждого указанного цилиндра, чтобы механические ключи точно выполняли требуемое открытые / не должны открывать отношения. Эта проблема сопоставления также NP трудна; на самом деле это проблема изоморфизма графовых подграфов [23, 37], см. раздел 3. С увеличением размера задачи детерминированные алгоритмы поиска [58, 59, 64, 65] быстро становятся неразрешимыми. В частности, стратегии сокращения графов, предназначенные для ограничения исчерпывающего изучения всего пространства поиска, как, например, введено в алгоритм VF2 [14, 15, 62], не дают существенного усиления для графов системы замков из-за высокой степени симметрии в механика. В качестве единственно возможной альтернативы, эвристическое исследование пространства поиска [2, 9, 46, 50, 55, 60] предлагает успешную парадигму, которая пытается извлечь выгоду из случайных вариаций для систематического поиска. Читатели, незнакомые или не убежденные в этой идее, могут быть склонны думать о том, чтобы торговать с (квази) уверенностью в очень долгом поиске обнадеживающего (хотя и в конечном счете неопределенного) шанса на достаточно быстрый успех. Как правило, каждый начинает с первоначального предположения, проверяет локальное соседство на наличие решения, а затем перезапускает при необходимости с другим предположением. Рандомизированное «угадывание» имеет решающее значение для инноваций или эволюции в глобальном поиске решения и может быть сделано либо неосведомленным, либо на основе идей, полученных из предыдущего опыта или упрощенных моделей, скажем. Кроме того, функция ошибки измеряет степень отклонения от оптимальной. Он может служить целевой функцией для методов оптимизации, таких как поиск типа «восхождение на гору» [55, 60] в локальных районах, или, по крайней мере, помочь определить, какие регионы глобального поиска являются более перспективными, чем другие.

Хотя ни одна методология поиска, основанная на вероятностной эвристике, не гарантируется как единообразно надежная или эффективная [69], тщательно подобранный алгоритм может все же достаточно быстро дать хорошие результаты во многих соответствующих практических случаях, чтобы быть полезным. Мы показываем, что среди большого класса алгоритмов стохастической оптимизации [9, 35, 46, 60], моделируемый отжиг [1, 2, 9, 12, 19, 33] может быть улучшен методами кодирования [11, 27, 28 , 36, 52], чтобы успешно справиться с проблемами в нашей обстановке, см. Разделы 4 и 5. Теперь мы приглашаем читателя сопровождать нас во вселенную замковых систем.

Этот ключ в нашем кармане, он также открывает мир на перекрестке алгебраической структуры, вычислительной сложности, комбинаторной оптимизации и рандомизированных алгоритмов.

Использованные источники

[1]  E. Aarts and J. Korst. Simulated Annealing and Boltzmann Machines. Wiley, 1988.

[2] E. Aarts and J. K. Lenstra. Local Search in Combinatorial Optimization. Princeton University Press, 2003.

[3] A. Aho, M. Garey, and J. Ullman. The transitive reduction of a directed graph. SIAM Journal on Computing, 1(2):131–137, 1972.

[4]  H. A¨ıt-Kaci, R. Boyer, P. Lincoln, and R. Nasr. Efficient Implementation of Lattice Operations. ACM Trans. Program. Lang. Syst., 11(1):115–146, 1989.

[5] P. R. Amestoy, I. S. Duff, and C. V¨omel. Task scheduling in an asynchronous distributed memory multifrontal solver. SIAM J. Matrix Anal. Appl., 26(2):544–565, 2005.

[6]  R. J. Anderson.  Security Engineering:  A Guide to Building Dependable Distributed Systems. Wiley, 2008.

[7] A. Auger and B. Doerr. Theory of Randomized Search Heuristics: Foundations and Recent Developments . World Scientific, 2011.

[8]  G. Birkhoff. Lattice Theory. Amer. Math. Soc., New York, Revised edition, 1948. [9]  E. K. Burke and G. Kendall. Search Methodologies. Springer, 2nd edition, 2014.

[10] Y. Caseau. Efficient Handling of Multiple Inheritance Hierarchies. SIGPLAN Not., 28(10):271– 287, 1993.

[11] Y. Caseau, M. Habib, L. Nourine, and O. Raynaud. Encoding of Multiple Inheritance Hierar- chies and Partial Orders. Computational Intelligence, 15:50–62, 1999.

[12] V. Cˇerny´. Thermodynamical approach to the traveling salesman problem: An efficient simula- tion algorithm. Journal of Optimization Theory and Applications, 45(1):41–51, 1985.

[13] P. Colomb, O. Raynaud, and E. Thierry. Generalized Polychotomic Encoding: A Very Short Bit-Vector Encoding of Tree Hierarchies. In Modelling, Computation and Optimization in Information Systems and Management Sciences, volume 14 of Comm. Comp.  Inf.  Sci., pages 77–86. Springer, 2008.

[14] L. P. Cordella, P. Foggia, C. Sansone, and M. Vento. An improved algorithm for matching large graphs. In 3rd IAPR-TC15 Workshop on Graph-based Representations Patt. Recogn., pages 149–159. 2001.

[15] L. P. Cordella, P. Foggia, C. Sansone, and M. Vento. A (Sub)Graph Isomorphism Algorithm for Matching Large Graphs. IEEE Trans. Patt. Anal. Mach. Int., 26(10):1367–1372, 2004.

[16] T. H. Cormen, C. E. Leiserson, R. L. Rivest, and C. Stein. Introduction to Algorithms. MIT Press, Cambridge (Mass.), London, 3rd edition, 2009.

[17] T. M. Cover and J. A. Thomas. Elements of Information Theory. Wiley, 2nd edition, 2006. [18]  B. A. Davey and H. A. Priestley.  Introduction to Lattices and Order.  Cambridge University Press, 2nd edition, 2002.

[19] A. Dekkers and E. Aarts. Global optimization and simulated annealing. Math. Prog., 50:367– 393, 1991.

[20] D. Ellerman. The Logic of Partitions: Introduction to the Dual of the Logic of Subsets. The Review of Symbolic Logic, 3:287–350, 2010.

[21]   L. Fennelly.  Effective  Physical  Security.  Butterworth-Heinemann, 4th edition, 2012.

[22]  N. Ferguson, B. Schneier, and T. Kohno.  Cryptography Engineering:  Design Principles and Practical Applications. Wiley, 2010.

[23]  M. R. Garey and D. S. Johnson.  Computers and Intractability:  A Guide to the Theory of NP-Completeness. W. H. Freeman, New York, 1979.

[24]  J. C. Giarratano and G. D. Riley.   Expert  Systems:   Principles  and  Programming.   Course Technology, 4th edition, 2004.

[25] B. Glover and H. Bhatt. RFID Essentials. O’Reilly Media, 2006. [26] F. Glover and M. Laguna. Tabu Search. Kluwer, 1997.

[27]  M. Habib and L. Nourine. Bit-vector encoding for partially ordered sets. In Orders, Algorithms, and Applications, volume 831 of LNCS, pages 1–12. Springer, 1994.

[28]  M. Habib, L. Nourine, O. Raynaud, and E. Thierry. Computational aspects of the 2-dimension of partially ordered sets. Theor. Comput. Sci., 312(23):401–431, 2004.

[29]  D. Henning and C. Reynolds.   Houdini: His Legend and His Magic. Times Books, NY, 1977.

[30]  L. H´erault, R. Horaud, F. Veillon, and J.-J. Niez.   Symbolic image matching by simulated annealing. In Proc. British Machine Vision Assoc., pages 319–324, 1990.

[31]  P. Jackson. Introduction To Expert Systems. Addison-Wesley, 3rd edition, 1998.

[32]  L. Jones and T. de Castella.   Is the traditional metal key becoming obsolete?    BBC News Magazine, October 30, 2014.

[33]  S. Kirkpatrick, C. D. Gelatt, and M. P. Vecchi. Optimization by simulated annealing. Science, 220(4598):671–680, 1983.

[34]  J. Kleinberg and E. Tardos. Algorithm Design. Pearson, 1st new international edition, 2013. [35]  B. Korte and J. Vygen.  Combinatorial Optimization:  Theory and Algorithms.  Springer, 5^th edition, 2012.

[36]  A.  Krall,  J. Vitek,  and  R.  Horspool.    Near  Optimal  Hierarchical  Encoding  of  Types.    In ECOOP’97 Obj.-Orient. Prog., volume 1241 of LNCS, pages 128–145. Springer, 1997.

[37] M. Kuramochi and G. Karypis. Frequent Subgraph Discovery. In Proc. 2001 IEEE Int. Conf. Data Mining, ICDM ’01, pages 313–320. IEEE Computer Society, 2001.

[38]  S. Kurutz. Losing the Key. The New York Times, June 12, 2014.

[39] A. Lawer. Calculation of Lock Systems. Masters degree project, trita-na-e04081, Royal Institute of Technology, Stockholm, Sweden, 2004.

[40]  R. Leighton and R. P. Feynman. Surely You’re Joking, Mr. Feynman! Vintage, 1992.

[41]  D. J. C. MacKay. Information Theory, Inference and Learning Algorithms. Cambridge, 2003.

[42] G. Markowsky. The representation of posets and lattices by sets. Algebra Universalis, 11(1), 1980.

[43] G. Markowsky. An overview of the poset of irreducibles. In Combinatorial and Computational Mathematics – Present and Future, pages 162–177. World Scientific, 2001.

[44]  M. McCloud, G. de Santos, and M. Jugurdzija.   Visual Guide to Lock Picking.   Standard Publications, 3rd edition, 2007.

[45]  Z Michalewicz.  Genetic Algorithms + Data Structures = Evolution Programs.  Springer, 3rd edition, 2008.

[46]  Z. Michalewicz and D. B. Fogel.  How to Solve It:  Modern Heuristics.  Springer, 2nd edition, 2004.

[47] C. Moore and S. Mertens. The Nature of Computation . Oxford University Press, 2011.

[48]   D. Ollam.  Practical Lock Picking,  Second Edition:  A Physical Penetration Tester’s Training Guide. Syngress, 2nd edition, 2012.

[49]  R. Paige and R. E. Tarjan. Three partition refinement algorithms. SIAM Journal on Comput- ing, 16(6):973–989, 1987.

[50]  C. H. Papadimitriou and K. Steiglitz. Combinatorial Optimization:  Algorithms and Complex- ity. Dover, 1998.

[51]  B. Phillips.  The Complete Book of Locks and Locksmithing.  McGraw-Hill Professional, 6th edition, 2005.

[52]  O. Raynaud and E. Thierry.  The Complexity of Embedding Orders into Small Products of Chains. Order, 27(3):365–381, 2010.

[53]  C. Robert and G. Casella. Monte Carlo Statistical Methods. Springer, 2nd edition, 2010.

[54]  S. Roman. Coding and Information Theory. Springer, 1992.

[55]  S. Russell and P. Norvig.  Artificial Intelligence:  A Modern Approach.  Pearson, 3rd edition, 2010.

[56]  P.  Salamon,  P.  Sibani,  and  R.  Frost.   Facts,  Conjectures,  and  Improvements  for  Simulated Annealing.  SIAM, 2002.

[57]   B. Schr¨oder.  Ordered Sets.  Birkh¨auser, 2003.

[58] J. G. Siek. An Implementation of Graph Isomorphism Testing, 2001.

THE SECRET LIFE OF KEYS: ON THE CALCULATION OF MECHANICAL LOCK SYSTEMS

CHRISTOF VO MEL, FLAVIO DE LORENZI, SAMUEL BEER,   ERWIN FUCHS