Канализационные системы являются важной частью современной инфраструктуры, и их надлежащее функционирование имеет важное значение. Тем не менее, во многих странах канализационные сети ухудшаются из-за их высокого возраста [11, 3, 2]. Поскольку восстановление и техническое обслуживание канализационных систем требуют огромных инвестиций (например, прочистка канализации в частном доме), большое внимание было уделено разработке методов контроля труб.
Оценка состояния канализационных труб обычно проводится путем визуального осмотра канализационных видеопоследовательностей. Тем не менее, ручная проверка имеет ряд недостатков, таких как субъективность, различные стандарты и высокие затраты. Ранее было предложено несколько подходов для автоматизации канализационных обследований. Например, было исследовано автоматическое обнаружение стыков труб и поверхностных трещин по цифровым канализационным изображениям [2]. В [14] был предложен метод автоматического определения стыков труб и анализа их формы. Идея восстановления трехмерной формы исследуемой трубы из видеоизображений была представлена в [3], где дополнительно был предложен метод определения положения камеры относительно центральной оси трубы. К сожалению, этот метод ограничен кирпичной канализацией с видимыми линиями раствора.
Были разработаны различные виды канализационных роботов, и некоторые из них содержат дополнительные датчики помимо видеокамеры [7, 11]. Например, в [7] для измерения формы поперечного сечения трубы использовалась дальномерная камера, использующая схему оптической триангуляции на основе лазера. Хотя мультисенсорные роботы предоставляют дополнительную информацию, они также приводят к более сложной и дорогой конструкции.
В этой статье мы предлагаем метод восстановления формы канализационной трубы исключительно из видеопоследовательности, полученной с помощью камеры с объективом с плоским глазом. Наш подход состоит в том, чтобы решить проблему структуры от движения в случае последовательностей изображений, полученных с помощью блеска, путем отслеживания точек интереса на последовательных изображениях. Мы опишем, как ограничения двух и трех видов между откалиброванными видами листа могут быть использованы при автоматическом восстановлении структуры. Это является важным дополнением к текущим методам структурирования от движения, поскольку, согласно нашим знаниям, ограничение трех видов ранее не использовалось в случае последовательностей изображений с плоским экраном. Например, недавняя работа Micusık [12] концентрируется на некалиброванной геометрии двух видов.
Обзор метода
Типичная система проверки канализации состоит из видеокамеры и трактора с дистанционным управлением. Такая система проиллюстрирована на рис. 1. У канализационного робота, который мы использовали, была камера с объективом «рыбий глаз», широкое поле зрения которой позволяет получать сканирование всей трубы с высоким разрешением за один проход.
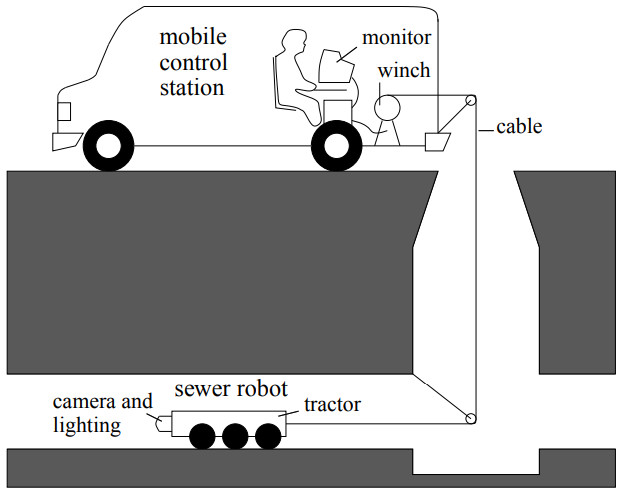
Наш подход к восстановлению структуры в основном следует структуре, представленной в [5]. Однако, поскольку обычная модель камеры с точечным отверстием не является действительным приближением к объективу с тонкой линзой, предлагается несколько важных модификаций. Далее мы кратко опишем различные этапы нашего метода.
1 Калибровка камеры
Хотя современный подход к восстановлению структуры часто не калибруется [5], мы применяем традиционный фотограмметрический принцип калибровки камеры перед измерениями. Одной из причин этого является особенность объектива «рыбий глаз», а другой – требование высокой точности.
Калибровка выполняется путем просмотра плоского калибровочного объекта, как описано в [10]. Поскольку соответствующая модель камеры очень гибкая, она подходит для объективов типа «рыбий глаз» с серьезными искажениями. Калибровка дает преобразование T, которое деформирует исходное изображение в перспективное, то есть преобразует координаты изображения «рыбий глаз» m tox˜ = T (m), которые являются нормализованными координатами изображения камеры-обскуры [10].
2 Извлечение и сопоставление функций
mˆ i = Pj (Xˆi). (2)
Отслеживаемые элементы – это точки интереса, обнаруженные детектором углов Harris, который широко используется в подобных приложениях. Эксперименты с канализационными видеопоследовательностями показали, что в эродированных бетонных трубах имеется множество таких особенностей. Обнаруженные точки интереса первоначально сопоставляются между каждой последовательной парой изображений посредством взаимной корреляции интенсивности окрестности.
3 Отслеживание функций
Предполагаемые точечные соответствия содержат почти неизбежно некоторые ложные совпадения. На этапе отслеживания цель состоит в том, чтобы использовать геометрические ограничения между последовательными парами видов и триплетами видов, чтобы управлять сопоставлением и отбрасывать ложные совпадения. Это требует некоторых модификаций к обычному способу оценки геометрии множественного вида [5]. Модификации необходимы для обеспечения обоснованного распределения ошибки оценки, когда соответствия изображений измеряются из исходных изображений типа «рыбий глаз» и м2.
Преобразованные координаты
x˜i = T (mi)
и между деформированными изображениями сохраняются отношения двух и трех видов, определяемые основной матрицей и трифокальным тензором.
Выводы
Мы предложили новый метод восстановления структуры сцены из последовательностей изображений «рыбий глаз» и применили его для измерения формы канализационных труб. Эксперименты показывают, что форма канализационной трубы может быть восстановлена исключительно из видеопоследовательности, которая сканируется за один проход по трубе. Кроме того, предлагаемая структура непосредственно применима к восстановлению структуры из любой видеопоследовательности, снятой калиброванной камерой, страдающей от серьезных искажений объектива, поскольку модель камеры [10] может гибко моделировать различные виды искажений. Следовательно, предлагаемый способ может быть использован в широком спектре потенциальных применений.
,
Использованные источники
[1] S. S. Brandt. On the probabilistic epipolar geometry. In Proc. BMVC, pages 107–116, 2004.
[2] M. J. Chae and D. M. Abraham. Neuro-fuzzy approaches for sanitary sewer pipeline condition assessment. J. Comput. Civil Eng., 15(1):4–14, January 2001.
[3] D. Cooper, T. P. Pridmore, and N. Taylor. Towards the recovery of extrinsic camera parameters from video records of sewer surveys. Mach. Vis. and Appl., 11:53–63, 1998.
[4] G. Csurka, C. Zeller, Z. Zhang, and O. Faugeras. Characterizing the uncertainty of the fundamental matrix. Comput. Vis. Image Underst., 68(1):18–36, 1997.
[5] A. W. Fitzgibbon and A. Zisserman. Automatic 3D model acquisition and generation of new images from video sequences. In Proc. European Signal Processing Conference, pages 1261–1269, 1998.
[6] A. W. Fitzgibbon and A. Zisserman. Automatic camera recovery for closed or open image sequences. In Proc. ECCV, pages 311–326, 1998.
[7] R. M. Gooch, T. A. Clarke, and T. J. Ellis. A semiautonomous sewer surveillance and inspection vehicle. In Proc. IEEE Intelligent Vehicles, pages 64–69, 1996.
[8] R. Hartley and A. Zisserman. Multiple View Geometry in Computer Vision. Cambridge, 2000.
[9] J. Kannala. Measuring the shape of sewer pipes from video. Master’s thesis, Helsinki University of Technology, 2004. [10] J. Kannala and S. Brandt. A generic camera calibration method for fi sh-eye lenses. In Proc. ICPR, pages 10–13, 2004.
[11] H.-B. Kuntze and H. Haffner. Experiences with the development of a robot for smart multisensoric pipe inspection. In Proc. IEEE Robotics and Automation, pages 1773–1778, 1998.
[12] B. Micˇusˇ´ık. Two-view geometry of omnidirectional cameras. PhD thesis, Czech Technical University, 2004.
[13] S. Umeyama. Least-squares estimation of transformation parameters between two point patterns. IEEE Trans. Pattern Anal. Mach. Intell., 13(4):376–380, 1991.
[14] K. Xu, A. R. Luxmoore, and T. Davies. Sewer pipe deformation assessment by image analysis of video surveys. Pattern Recognit., 31(2):169–180, 1998.
Measuring the Shape of Sewer Pipes from Video
Juho Kannala, Sami S. Brandt